As the sample size increases, the distribution of the data tends to become more normal. This is due to the Central Limit Theorem, which states that as the sample size gets larger, the distribution of the data will become more and more normal.
Checkout this video:
The Basics of Sampling
It is important to understand the basics of sampling when conducting research. Probability sampling is a method of sampling that uses random selection to choose members of a population to participate in a study. A population is the entire group of items from which the sample is drawn. The sample is a subset of the population. The purpose of probability sampling is to select a sample that is representative of the population.
What is sampling?
In statistics, sampling is the process of selecting a group of items from a larger population. The target population is the total set of individuals from which the sample might be drawn. A common goal of sampling is to infer properties of the target population based on analysis of the sample.
Sampling can be used for both statistical inference (drawing conclusions about a population from a sample) and estimation (coming up with an estimate of a population parameter based on a sample). Sampling can also be used to track changes over time in a population.
There are different types of sampling: probability and non-probability. Probability sampling methods include:
-Simple random sampling: This is where each member of the population has an equal chance of being selected for the sample.
-Stratified random sampling: This method involves dividing the population into groups (strata) and then selecting a random sample from each stratum.
-Cluster sampling: This method involves dividing the population into groups (clusters) and then selecting a complete sample from at least one group.
-Systematic sampling: This method involves selecting members of the population at fixed intervals.
Non-probability sampling methods include:
-Convenience sampling: This is where members of the population are selected because they are easy to reach or have agreed to participate.
-Purposive sampling: This is where members of the population are selected deliberately because they have some characteristic that makes them suitable for inclusion in the sample.
What is the difference between a population and a sample?
A population is the entire group of items from which a sample might be selected. A sample is a subset of the population. It is important to remember that, when we take a sample, we are usually interested in understanding something about the larger population from which it was drawn.
There are two main types of sampling: probability and non-probability sampling. Probability sampling is when each member of the population has a known and equal chance of being selected for the sample. Non-probability sampling is when the chances of different members of the population being selected are not known or they are not equal.
Why is sampling important?
Sampling is important because it allows us to make inferences about a population based on a smaller, more manageable data set. In other words, it allows us to extrapolate from the data we have to the data we want.
There are many different ways to sample from a population, and the method you choose should be based on your specific research objectives. Some common methods include convenience sampling, random sampling, systematic sampling, and stratified sampling.
The Different Types of Sampling
Probability theory and statistical inference rest on the assumption that a population exists from which a sample can be taken. This population may be finite or infinite. The sample space of a random experiment is the set of all possible outcomes of that experiment. The distribution of a random variable is a probability distribution that assigns a probability to each measurable subset of the sample space. In this section, we will explore the different types of sampling.
Probability Sampling
Probability sampling is a statistical method used to select a random sample from a population. The advantage of probability sampling is that it allows researchers to make inferences about a population based on the results of the sample. The disadvantage is that it can be time-consuming and expensive to select a truly random sample.
There are several types of probability sampling, including:
-Simple Random Sampling: This is the most basic type of probability sampling. A simple random sample is one in which each member of the population has an equal chance of being selected. This can be done by using a random number generator or by selecting members of the population at random (e.g., using a coin toss).
-Systematic Sampling: In systematic sampling, members of the population are selected at regular intervals. For example, if you wanted to select a random sample of 100 people from a population of 1000, you could select every 10th person on a list of all 1000 individuals.
-Stratified Sampling: Stratified sampling is a type of probability sampling in which the population is divided into subgroups (strata) and a separate random sample is selected from each subgroup. This type of sampling is often used when there are known differences between subgroups in the population (e.g., gender, age, ethnicity).
-Cluster Sampling: Cluster sampling is similar to stratified sampling, but instead of selecting a separaterandom sample from each subgroup, clusters of members are selected at random and all members of those clusters are included in the study. Cluster sampling is often used when it would be too costly or impractical to select a simple random sample from an entire population.
Non-probability Sampling
Non-probability sampling is a sampling method where samples are gathered in a manner that does not give all individuals in the population an equal chance of being selected. Because of this, non-probability samples should not be used to make inferences about a population, as they are likely to be biased.
There are four main types of non-probability sampling: convenience sampling, purposive sampling, quota sampling, and snowball sampling.
Convenience Sampling: Convenience sampling is a type of non-probability sampling where the first individuals who come to mind or who are easily accessible are chosen as part of the sample. This type of sampling is often used in market research, as researchers can simply approach people in public places and ask them to participate. However, because this type of sampling relies on chance, it is often not representative of the population and can lead to bias.
Purposive Sampling: Purposive sampling is a type of non-probability sampling where individuals are chosen based on specific characteristics that they possess. For example, if a researcher was interested in studying doctors who have experience with a particular medical condition, they would use purposive sampling to select participants. While this type of sampling can be useful for studying specific groups of people, it also runs the risk of bias if the researcher’s selection criteria are not met.
Quota Sampling: Quota sampling is similar to convenience sampling in that it relies on accessibility, but with quota sampling, individuals are chosen so that the sample represents specific proportions of the population. For example, if a researcher wanted to study a classroom of students and wanted their sample to include 50% males and 50% females, they would use quota sampling. However, quota samples can also be biased if the quotas are not met or if the individual chosen to fill a quota does not accurately represent the group they are supposed to represent.
Snowball Sampling: Snowball sampling is a type of non-probabilitysampling where initial participants provide referrals for future participants. This type ofsampling is often used when researching hard-to-reach populations, such as specific minorities or social groups. However, this method can also lead to bias if the initial participants do not accurately represent the population as a whole.
The Effect of Sample Size on the Shape of the Distribution
When you increase the sample size, the shape of the distribution changes. This is due to the Central Limit Theorem . The Central Limit Theorem states that as the sample size increases, the distribution of the data will become more normal.
Central Limit Theorem
In probability theory, the central limit theorem (CLT) states that, given certain conditions, the mean of a sufficiently large number of independent random variables, each with a well-defined (finite) expected value and variance, will be approximately normally distributed, regardless of the underlying distribution. The central limit theorem has a number of variants. In its simplest form, the random variables can be assumed to be identically distributed. However, in many applications it is possible to allow for non-identical distributions and still apply the central limit theorem by using additional conditions such as independence.
The central limit theorem is one of the most important results in all of probability theory because it establishes a link between the properties of a distribution function and the behavior of its Sample mean.
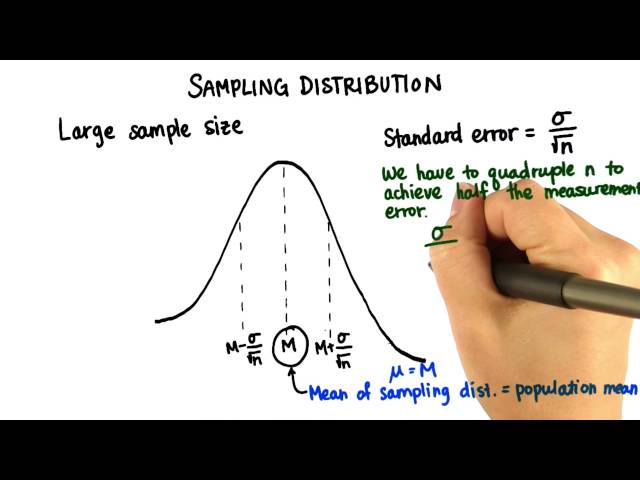
Sampling Distribution of the Mean
As the sample size increases, the shape of the sampling distribution of the mean approaches a normal distribution. This is because as the sample size increases, the variability of the distribution decreases.
Sampling Distribution of the Proportion
In statistics, it’s important to understand the sampling distribution of a statistic. The sampling distribution is the set of all possible values that the statistic can take on, given a set of data. The shape of the sampling distribution can give you information about the underlying population.
As the sample size increases, the shape of the sampling distribution of the proportion will become more and more normal. This is because, as the sample size increases, the Central Limit Theorem kicks in and tells us that the sum of a large number of random variables will be approximately normal, regardless of the underlying distribution.