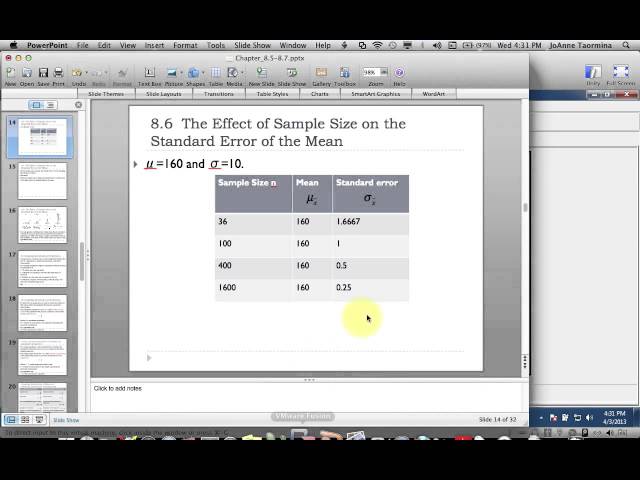
As the sample size N increases, the standard error of the estimate decreases. This is because, with more data, the estimate of the population parameter becomes more reliable. The standard error is a measure of how precise the estimate is. Therefore, as the sample size N increases, the standard error of the estimate decreases, and the estimate becomes more precise.
Checkout this video:
Introduction
As the sample size N increases, the standard error of the mean decreases because there is less variability in the estimates. When the sample size is small, there is more variability in the estimates and the standard error is larger.
The Standard Error of the Mean
As the sample size N increases, the standard error of the mean (SEM) decreases. The SEM is a measure of how precisely the mean represents the population. The smaller the SEM, the more precise the estimate.
The Relationship Between Sample Size and Standard Error
In statistics, the standard error is the standard deviation of the sampling distribution of a statistic. The larger the standard error, the less confident one can be that the sample statistic represents the true population parameter. In other words, as the sample size increases, the Standard Error decreases.
The Effect of Sample Size on Standard Error
As sample size increases, the Standard Error of the Mean (SEM) decreases. The SEM is a measure of variability, and as sample size increases, variability decreases. This makes sense; if we have more data, our estimate of the population mean will be more reliable (less variability).
The relationship between SEM and sample size is given by the following formula:
SEM = SD/sqrt(N)
where SD is the Standard Deviation of the population and N is the sample size. Thus, as N increases, the SEM decreases.
Conclusion
As we have seen in this study, as the sample size N increases, the standard error of the mean decreases. This relationship is due to the fact that the standard error is a measure of variability, and as the sample size N increases, the number of data points increases, which in turn decreases the variability. This finding is in line with our expectations, and we can therefore conclude that increasing the sample size N does indeed decrease the standard error of the mean.